原文鏈接:https://mp.weixin.qq.com/s/1A0Jq84kCqLAyGdIkfXBUw
原文題目:PAIRWISE LINKAGE FOR POINT CLOUD SEGMENTATION
摘要:在本文中,我們首先提出了一種新穎的分層聚類算法,稱為(P-Linkage),該算法可用于對任意維的數據進行聚類,然后將其有效地應用于無序3D點云分割。P-Linkage聚類算法首先計算每個數據點的特征值,例如2D數據點的密度和3D點云的平坦度。然后,對于每個數據點,依據特征值大小創建查詢點和k近鄰點之間成對鏈接。通過以這種搜索鏈接的方式,可以進一步發現其他聚類。最后,合并所有的聚類完成分割。
Introduction
分割是點云處理中重要的預處理步驟之一,是將數據點分類和標記為多個單獨的組或區域的過程,每個組或區域對應于對象表面的特定形狀。
1.1 Point cloud segmentation
3D點云分割并不容易,因為三維點數據通常不完整,稀疏分布且沒有拓撲結構,而且對點的統計分布也沒有先驗知識。針對點云分割,目前的方法可以大致分為三大類:基于邊界,基于區域增長和混合方法。
基于邊界的方法嘗試檢測形成閉合邊界的不連續性,然后將點分組到已標識的邊界和連接的邊緣內。這些方法通常適用于深度圖,將局部表面超過給定閾值的點定義為邊界。最常用的局部表面特性是表面法線,梯度,主曲率或高階導數(Sappa和Devy,2001;Wani和Arabnia,2003)。但是,由于激光掃描儀本身引起的噪聲或3D空間中空間上不均勻的點分布,此類方法通常會檢測到不連續的邊緣,導致封閉邊界區域的識別工作效果不佳(Castillo等,2013)。
基于區域增長的方法通過檢測連續表面的幾何特性來完成分割。在無序3D點云的分割中,這些方法首先選擇種子點,如果種子點和鄰近點在表面點屬性(例如方向和曲率)具有相似性,則將其與種子點聚類(Rabbani et al。,2006,Jagannathan and Miller,2007)。還有一些算法將子窗口(Xiao等,2013)或線段(Harati等,2007)作為種子點。(Woo et al。,2002)提出了一種基于八叉樹的3D網格方法來處理大尺度無序點云。能夠平滑連接區域是基于區域增長方法的關鍵。廣泛使用表面法線和曲率約束條件來找到平滑連接的區域(Klasing等,2009;Belton和Lichti,2006)。一般情況下,由于使用了全局信息,基于區域增長的方法比基于邊緣的方法對噪聲更加魯棒(Liu和Xiong,2008)。但是,這些方法對初始種子區域的位置很敏感,區域邊界附近點的法線和曲率的不正確估計會導致分割結果不準確,并且離群點還會導致過分割或欠分割。
混合方法同時使用基于邊緣/邊界的方法和基于區域增長的方法,以克服各前兩個方法的局限性(Vieira和Shimada,2005;Lavouée等,2005)。Benk?o和V′arady,2004年)提出了一種用于工程對象分割的混合方法,該方法首先使用基于邊緣的方法檢測銳利邊緣,然后在濾除銳利邊緣后找到平滑區域并混合。但是,這些混合方法的好壞取決于采用的單個方法的效果。
1.2 Clustering
聚類分析旨在基于元素的相似性將其分類,已應用于許多領域,例如數據挖掘,天文學和模式識別。通常,這些算法可以分為兩類:分區方法和分層方法。分區聚類算法通常通過某種相似性度量將每個數據點分類為不同的聚類。傳統的算法K-Means(MacQueen等,1967)和CLARANS(Ng和Han,1994)屬于這一類。分層方法通常通過將數據集迭代拆分為較小的子集,直到每個子集僅包含一個對象,從而創建數據集的分層分解,例如,單鏈接(SLink)方法及其變體(Sibson,1973)。
1.3 Clustering in Point Cloud Segmentation
基于元素的相似度,將元素分類的聚類算法也可以應用于3D點云的分割。廣泛使用的K-Means算法(MacQueen等,1967)將數據點劃分為K個(給出簇數的預定義參數),K-Means聚類算法的缺點是它需要事先知道聚類簇的數量,但在許多情況下無法預先定義。為了克服這一缺點,在點云分割中采用了均值漂移算法(Comaniciu和Meer,2002),該算法是一種通用的非參數技術,用于對分散的數據進行聚類(Yamauchi等,2005b;Yamauchi等,2005a,Zhang等,2008)。在(Yamauchi等,2005b,Yamauchi等,2005a)的工作中,均值漂移算法分別用于積分網格法線和高斯曲率的整合。在(Liu and Xiong,2008)的工作中,將法線方向轉換為高斯球體,并提出了一種新穎的單元均值漂移算法,以無參數的方式識別平面,拋物線形,雙曲線形或橢圓形表面。但是,大多數基于聚類的點云分割方法只能發現少量分割,這種分割可以在某些行業應用中使用,但在包含數大量數據的室內和室外激光掃描儀點云上可能會失敗。
1.4 Objectives and MotivationSegmentation
在本文中,我們提出了一種簡單,有效的點云分割算法,該算法通過在點云分割上應用聚類算法,可以應用與無序點云。引入兩個概念:
P-Linkage Clustering:基于以下假設:數據點應與其最接近的相鄰點(CNP)處于同一群集中,而最接近的相鄰點(CNP)更有可能成為群集中心,我們提出了一種新穎的分層成對方法,稱為成對鏈接(P-Linkage),它以簡單有效的方式發現集群。首先,應用成對鏈接程序將每個數據點在數據點級別鏈接到其CNP。然后可以通過從具有最大局部密度的點開始沿成對鏈接搜索來發現初始聚類,提出的聚類方法不是迭代的,一般情況下只需要一步,針對特定情況也提出了一種聚類方法。
Point Cloud Segmentation:基于提出的P-Linkage聚類,我們開發了一種簡單高效的點云分割算法,該算法僅需一個參數,即可應用于大量非結構化的車載,空中和固定式激光掃描儀點云。點云分割中的P鏈接聚類將3D點的估計曲面的平坦度作為其特征值,并通過沿鏈接的點集合收集來形成初始聚類。對于每個初始集合,我們創建一個切片。所有切片均以簡單或有效的方式進行合并以獲得最終的分割結果。所提出的點云分割算法只需要一個參數就可以平衡平面和曲面結構的分割結果。
2 PAIRWISE LINKAGE
P-Linkage聚類方法的關鍵概念是:數據點pi應該與最接近的鄰居pj位于同一個群集中,而最鄰近的鄰居pj更有可能成為群集中心,并且pi和pj之間的這種關系稱為成對鏈接。此概念源自非最大抑制(NMS)的概念(Canny,1986;Neubeck和Van Gool,2006),其中僅需要用一個數據點與其鄰居進行比較,如果密度不是最大,則抑制。圖1顯示了NMS的原理,從中我們可以看到p1被p2抑制,并且與p3相比,p2受到相同的抑制,這導致鏈接p1→p2→p3。通過這種方式,曲線上的所有數據點最終都可以通過與相鄰點的比較而鏈接到聚類中心c,它是局部最大值。實際上,P-Linkage聚類彌補了數據點的局部信息與全局信息之間的差距,這使其比基于局部的聚類方法更魯棒,并且比基于全局的聚類方法更高效。
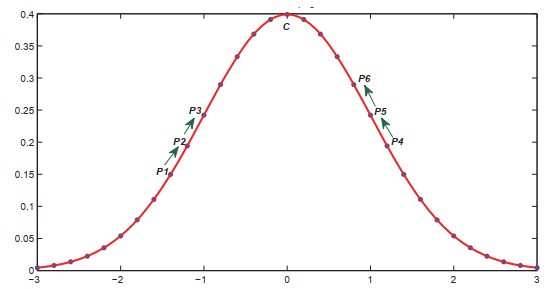
圖1 2維高斯曲線上的成對鏈接的插圖。從NMS派生而來,PLinkage將每個數據點與其相鄰點進行比較,并形成從p1→p2→p3 ...→c的鏈接。
基于2D數據點聚類的成對鏈接算法以數據點的密度為其特征值來建立鏈接。主要概念如下:
Cutoff Distance:如圖2所示,截止距離dc是一個全局參數,用于將數據點pi的鄰域集與其他數據點區分開。在(Rodriguez和Laio,2014)的最新工作中,將dc的值設置為任意兩個數據點之間的所有距離(表示為集合D)的所有距離的前1%-2%值的升序排列。但是,以這種方式設置截止距離dc是不合適的,因為dc是相鄰點分布的指標,應該從局部鄰域而不是D中得出。因此,我們提出了一種簡單的方法來確定dc的值,如下所述。對于每個數據點pi,將pi與它的最近鄰居之間的距離記錄在Dcn中,然后將dc計算為:
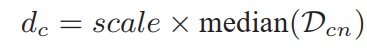
其中scale是自定義參數,這意味著截止距離dc是scale乘以設置Dcn的中值的值。這樣,dc表示的鄰域分布信息要比將其設置為D的1%-2%多得多。只有將到pi的距離小于dc的數據點視為pi的鄰域集,記為Ii,綠色圓圈如圖2所示。
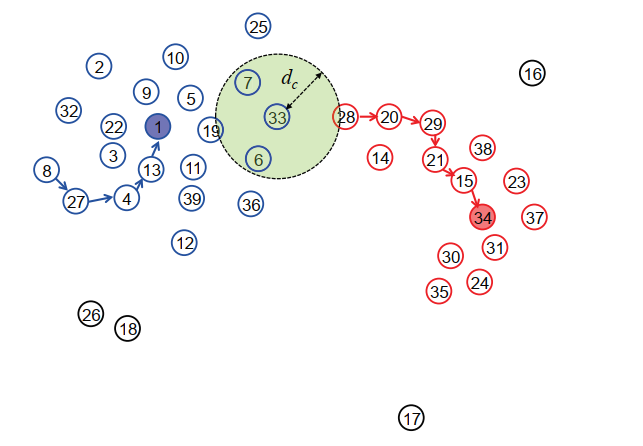
圖2分層聚類過程的說明。數據點p1和p34是聚類中心,符號→表示成對鏈接,綠色的大圓圈表示具有截止距離dc的數據點的鄰域集
Density:(Rodriguez和Laio,2014年)將數據點pi的密度定義為其鄰居數據點的數量,該值是離散值,因此不適合我們需要連續值密度的應用。在我們提出的方法中,數據點pi的密度ρi是通過在所有數據點上應用高斯核來計算的,如下所示:
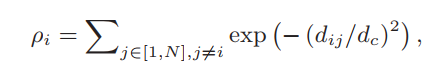
其中N表示所有數據點的數量,dij是兩個點pi和pj之間的距離。
Pairwise Linkage: 利用所有數據點的密度,可以以非迭代的方式恢復成對的鏈接,方法如下。對于鄰域為Ii的數據點pi,我們遍歷Ii中的每個點,并找到密度大于pi的最近數據點pj,然后我們認為數據點pi應該與pj在同一簇中,并且記錄數據點pi和pj之間的鏈接。如果pi的密度是局部最大值,這意味著Ii中不存在密度大于pi的數據點,則我們將pi視為聚類中心。成對鏈接過程的結果由記錄鏈接關系的查找表T和記錄所有聚類中心的集合Ccenter組成。
Herarchical Cluctering: 分層聚類是自上而下的過程,類似于分裂聚類算法的過程。對于Ccenter中的每個群集中心ci,我們開始以深度優先或廣度優先的方式從ci搜索查找表T,以收集與ci直接或間接連接的所有數據點,從而生成一個以ci為中心的群集。整個層次聚類找到最終的聚類C。圖2顯示了層次聚類過程的圖示。從圖2中,我們可以看到p1是其局部最大密度而成為聚類中心,并且在(p1,p13),(p13,p4),(p4,p27)和(p27,p8)之間存在四個成對鏈接。因此,按照p1→p13→p4→p27→p8進行層次聚類。通過這種方式,聚類信息從密集的數據點傳播到稀疏的數據點,這類似于熱傳播。
Cluster Meraging: 如圖1所示,當數據點呈高斯分布時,通過成對鏈接的層次聚類可以找到全局聚類中心并很好地恢復聚類,但是當存在一個或多個局部最大值時,聚類結果可能會失敗。為了應對數據點分配的所有條件,提出了一種定制的集群合并策略,該策略包括以下三個步驟。首先,對于每個群集C p,計算Cp中所有數據點的平均密度μp和標準偏差σp。其次,通過搜索相鄰簇之間的邊界數據點來收集每個簇Cp的相鄰簇。對于Cp中的每個數據點pi,其鄰域集表示為Ii。如果Ii中的數據點pj屬于另一個簇Cq,則將這兩個簇視為一對相鄰簇,將pi和pj分別記錄為Cp和Cq之間的相鄰點。
第三,對于每個相鄰的簇對Cp和Cq,Cp和Cq的相鄰點的平均密度分別表示為ρp和ρq。如果滿足以下條件,將合并這兩個相鄰的群集:
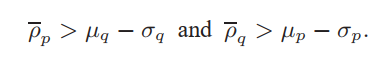
群集合并以迭代方式進行,這意味著將直接或間接與起始群集相鄰的所有群集合并。
Outliers: 在(Ester等人,1996)提出的以前的工作中,離群點是那些密度小于某個閾值的點。通過這種方式,低密度數據點可以被分類為離群值。在(Rodriguez and Laio,2014)的工作中,離群點被認為是密度小于群集邊界區域中最高密度的那些異常點,這意味著將丟棄群集邊界區域中的所有數據點作為離群值。在我們的工作中,我們考慮群集級別的異常值。如果密度為局部最大但小于所有數據點的中值密度中位數(ρ)的數據點pi,則將具有pi的同一群集中的所有數據點視為異常值。
圖2展示了所提出的P-Linkage方法的一些基本思想,從中我們可以觀察到分別有藍色和紅色兩個簇。對于每個數據點,通過搜索密度大于其自身密度的最近鄰點來形成成對鏈接。例如,首先將p8鏈接到p27,然后將p27鏈接到p4,再將p4鏈接到p13,最后將p13鏈接到p1,并且在其附近密度最大。通過這種方式,可以找到完整的鏈接,即p8→p27→p4→p13→p1,因此所有這五個數據點都被歸類為同一聚類,其聚類中心為p1。對于所有藍色的數據點(作為單獨的群集),將執行相同的過程。類似地,紅色簇可以通過這種方式形成。至于兩個聚類之間邊界上的數據點,仍然可以應用成對鏈接。以數據點p33為例,p19,p7,p6和p28是其鄰近點,p6是其最鄰近點(CNP),因此p33被分類為藍色簇,這是非常合理的。黑色的四個數據點p26,p18,p17和p16被歸類為離群值,因為它們的鄰域中不存在CNP,并且它們的聚類中心的密度也不足夠高。
綜上所述,所提出的聚類方法在通常情況下僅需一步即可發現聚類和聚類中心,而無需合并過程。對于每個具有密度ρi的數據點pi,我們找到其密度大于pi的最接近的相鄰點CNP(pi),并將該點pi分類為與CNP(pi)相同的群集。如果數據點pi的密度ρi是局部最大值并且大于平均密度ρ,則我們將pi視為聚類中心。算法1詳細描述了建立P鏈接聚類方法的完整過程。

3 P-LINKAGE FOR POINT CLOUD SEGMENTATION
點云的分割也可以表述為聚類問題,因為小表面上的數據點通常共享相似的法線值。因此,我們可以在點云的分割上采用建議的P-Linkage聚類方法,該方法在兩個方面與2D數據點的分割有所不同:(1)鄰域基于K最近鄰(KNN)而不是固定距離(2)特征值是估計表面的平整度而不是鄰域的密度;(3)將兩個數據點法線方向的偏差作為度量而不是其歐幾里得距離。在以下小節中,我們將詳細說明基于P鏈接的點云分割算法。
Normal Estimation:在本文中,我們采用KNN方法查找每個數據點的鄰域,并通過主成分分析(PCA)估算鄰域表面的法線。該過程包含以下三個步驟。首先,我們通過應用ANN庫構建k-d樹(Mount and Arya,2010)。對于每個數據點pi,找到其K個最近鄰居(KNN)并將其記錄為Ii,并根據它們到pi的距離按升序排序。其次,對于每個數據點pi,協方差矩陣由其KNN集Ii中的前K / 2個數據點形成,如下所示:
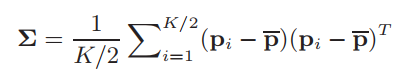
其中Σ表示3×3協方差矩陣,p表示Ii中前K / 2個數據點的平均矢量。然后是標準特征值方程:
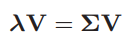
對于每個數據點,我們首先找到它的K個最近鄰居,然后通過PCA通過第一個K/2個鄰居計算其特征向量,然后將特征向量v0作為法線,將特征值λ0作為估計平面的平坦度。之后,采用最大距離最小一致性算法(MCMD)(Nurunnabi et al,2015)查找內部值和異常值,中值絕對偏差(MAD)的計算如下:
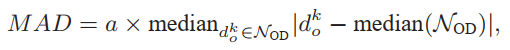
Rz權重為:
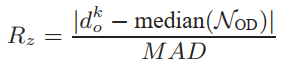
小于恒定閾值2.5(Nurunnabi et al,2015)。因此,對于每個數據點pi,我們獲得其法線n(pi),平坦度λ(pi)和一致集CS(pi)。
Linkage Building: 利用所有數據點的法線,平坦度和CS,可以以非迭代的方式恢復成對鏈接,方法如下。對于每個數據點pi,我們在其CS中進行搜索以找出平坦度小于pi的鄰居,并從中選擇法線與pi具有最小偏差的鄰近點作為CNP(pi)。如果存在CNP(pi),則會在CNP(pi)和pi之間建立成對鏈接并將其記錄在查找表T中。如果pi的平坦度λ(pi)在其附近最小,并且λ(pi)超過以下閾值:
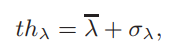
則將pi作為聚類中心,并將其插入群集中心Ccenter的列表中。 Slice Creating: 為了創建表面切片,首先通過從Ccenter中的每個聚類中心沿著查找表T搜索以形成聚類C,以收集與其直接或間接連接的數據點。數據點數小于10的群集將作為異常值被刪除。然后,對于每個聚類C p,通過(Nurunnabi et al,2015)提出的MCS方法通過平面擬合創建一個切片,這是一個迭代過程,迭代次數計算為:
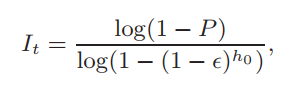
迭代后,按升序對S(λ0)進行排序,然后選擇與最小平坦度對應的平面作為Cp的最佳擬合平面。
然后,應用MCMD離群值消除方法找出與Cp最佳擬合的平面的離群值,也稱為一致性集(CS)。因此,對于每個切片Sp,我們以與每個數據點相同的方式獲得其法線n(Sp),平坦度λ(Sp)和一致集CS(Sp)。
Slice Merging:為了獲得在室內和工業應用中非常普遍的完整平面和曲面,提出了一種有效的切片合并方法,該方法類似于PLinkage群集中引入的群集合并過程,并包含以下步驟。首先,我們搜索每個切片的相鄰切片,如果滿足以下條件,則將兩個切片Sp和Sq視為相鄰切片:

然后,對于切片Sp及其相鄰切片Sq之一,如果滿足以下條件,它們將被合并:
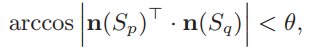
4 EXPERIMENTAL RESULTS
P-Linkage唯一需要的自定義參數是用于確定dc值的比例。為了評估在高斯分布數據上提出的方法,我們在“形狀集”1中選擇了兩個測試數據,分別包含15個和31個聚類。圖3顯示了它們的聚類結果,其中黑點代表離群值,其他不同顏色的點屬于不同的聚類。
我們可以看到,在兩個數據集中,所有聚類均被正確發現,并且所提出的方法提取的離群值都是合理的。
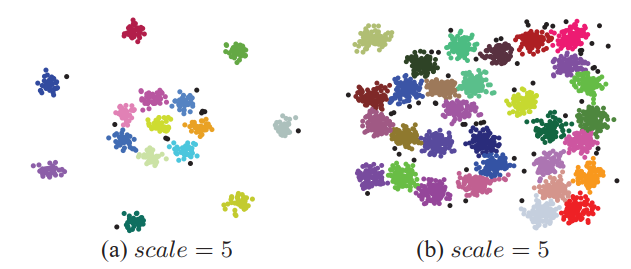
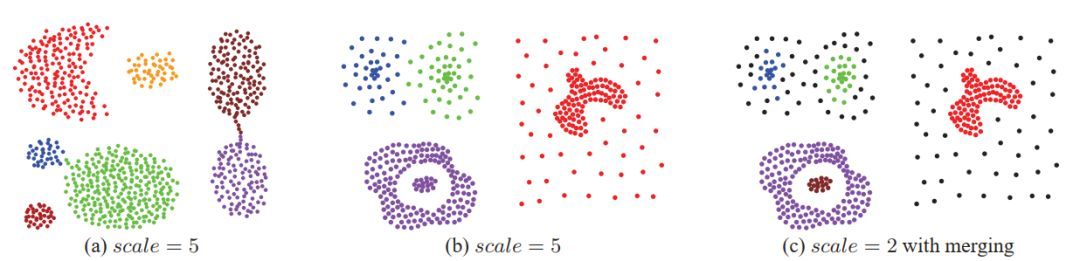

圖5該方法在3D(XYZ)模擬測試數據上的聚類結果:原始數據點和聚類結果從左到右投影到XY平面,YZ平面和XZ平面上
所提出的P-Linkage聚類可以直接用于存在大量的數據點場景點云的分割等應用,為了測試所提出的點云分割方法的魯棒性,我們將其應用于車載,空中和固定式激光掃描儀點云。


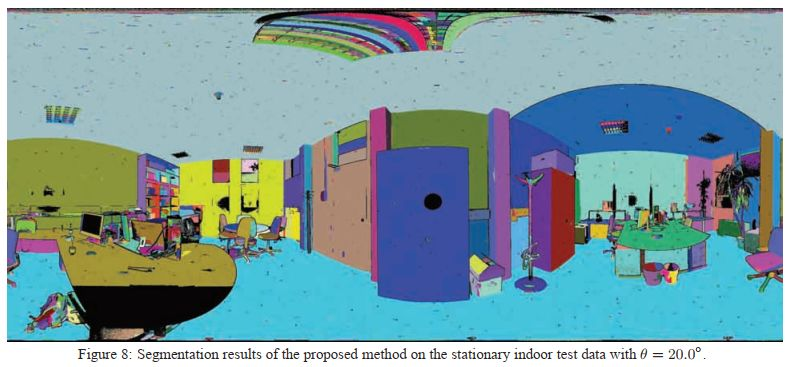
5 CONCLUSION
在本文中,我們提出了一種新的名為P-Linkage的分層聚類方法,通過在數據點上的成對鏈接,以一種簡單有效的方式發現聚類。提出的P-Linkage聚類可以直接用于具有大量聚類和復雜場景的點云。我們提出了一種高效的點云分割算法,該算法可以處理從不同場景捕獲的大量數據點。從2D到4D的不同數據的實驗結果充分證明了所提出的P-Linkage聚類算法的效率和魯棒性,并且在車載,空中和固定式激光掃描儀點云上的大量實驗結果充分說明了魯棒性和可靠性。