本文轉自集智俱樂部

如何理解復雜系統?如何分析復雜系統?如何設計復雜系統?這是研究和學習復雜性科學會遇到的問題。美國新英格蘭復雜系統研究所(New England Complex Systems Institute, NECSI)的 Yaneer Bar-Yam(創始人及所長)和 Alexander F. Siegenfeld 近期撰文,梳理了復雜性研究的共識,全面介紹了復雜系統科學這一領域的基本原理、常用方法和應用方向。
這篇長文綜述的目標,是幫助具有高中數學水平的社會大眾,理解復雜系統和社會現實。我們翻譯了全文,供各領域學者、工業界、政府和慈善組織的決策者參考。針對部分關鍵概念,我們在文中補充了譯注。

論文題目:
An Introduction to Complex Systems Science and its Applications
論文地址:
https://necsi.edu/an-introduction-to-complex-systems-science-and-its-applications
很多概念和定量的分析框架所基于的標準假設對于眾多復雜的物理、生物和社會系統并不滿足。復雜系統科學可以告訴我們這些假設在什么情況下失效,以及為什么失效,并提供了可以理解復雜系統屬性的另一個框架。本綜述介紹了復雜系統科學的一些基本概念,包括復雜度曲線,有效性和適應性的權衡,系統復雜度和環境復雜度匹配的必要性,多尺度分析以及進化過程。復雜系統科學的目的是對系統一般屬性的理解和討論,而不是對于具體系統動態的建模。相對于提供全面的綜述,本文更希望是來科普一些可用于對我們世界里的復雜系統進行理解和應用的簡單概念和分析方法。本文將以簡單的語言進行,只需要高中層次的數學和科學背景即可,以便讓各個領域的學者與各個行業、各級政府和慈善機構的決策者以及其他任何對系統和社會感興趣的人都可以看懂。
引言
我們應該如何科學地研究物理、生物和社會等復雜系統?實證研究雖然有用,但它們本身還不夠,因為所有實驗都需要一個可以解釋它們的理論框架。盡管當前存在許多這樣的框架來理解系統的特定組成部分或方面,但大多數定量研究所依據的標準假設通常并不適用于整個系統層次,從而導致大尺度行為的原因和后果被錯誤地描述。
本文對復雜系統科學進行了介紹,展示了它的一些應用,它能幫助我們在周邊復雜系統中進行有效決策。復雜系統科學著重于復雜系統的一般屬性,而不是像動態系統、多主體建模、網絡科學和混沌理論等子領域中對特定動態行為的建模。第II 節介紹了關鍵概念,包括復雜度曲線,效率與適應性之間的此消彼長以及使系統的復雜度與其環境復雜度相匹配性的必要性。本文第III 節討論了對復雜系統的分析,關注了一個經常被忽略的問題,即標準假設何時適用何時不適用(不適用的情況更加重要)。第IV 節討論了一些有效干預復雜系統的原則,即使它們的完整描述通常超出了人類的理解范圍。第V節進行總結。
第一部分、復雜系統科學中的基本原理 (BASIC PRINCIPLES OF COMPLEX SYSTEMS SCIENCE)
A. 為什么要復雜系統科學(Why complex systems science)?
復雜系統科學研究的對象是包含很多構成組元(components)的系統,范圍極廣,包括物理系統、生態系統和社會系統等。但不像其他學科那樣關注構成系統的組元本身,復雜系統科學關注的是系統中的組元是如何關聯起來的。如圖1所示,不同的列分屬不同的學科,如物理學科會研究雪花、炮彈彈道、氣體這些由分子構成不同對象,而復雜性科學研究會從橫向上綜合來進行,如一群氣體分子、一群生物、一群人這些系統的共同規律。系統的性質主要取決于其組元的關系,而不是組元本身[1]。復雜系統科學的目的是提供統一的科學框架,允許思想的泛化(和在此基礎上的銳化),促使新應用、新連接的發現。
[1]譯者注:我們學過物理的人知道,無論動物和植物,都是由有限種類的原子構成,再微觀一些就是6種夸克和6種輕子。但動物和植物具有不同的功能。即使是同一類生物,個體之間的差別也很大,其原因在于其物質的組合形式不同。
即使有一個非常簡單的系統,要想對其所有的細節進行完整的描述也是不可能的。好的分析研究需要尋找那些并不依賴于所有細節的系統屬性。這種屬性是存在的,因為復雜系統往往具有普適性 (Universal-Examples of Behaviorsity)[2]。統計物理科學告訴大家人類有洞察這種系統特征的能力。統計物理上,嘗試刻畫系統特定狀態的行為(例如一個氣體系統)是一個艱巨的不可能的任務,但刻畫所有可能狀態的集合不僅容易處理,而且還可以為我們提供相關信息的模型(例如壓力,溫度,密度,可壓縮性等)。這是一個功能強大的分析視角,不僅可以應用于物理系統,也可用于生物系統和社會系統。比如,熵 (entropy) 是物理學的一個重要概念,它描述系統可能狀態的數量。復雜系統科學所關注的系統的復雜度 (complexity) 或者復雜性程度,本質上就是一種廣義熵。
[2]譯者注:方福康教授曾指出:“在復雜系統中所涉及的一些基本特征,如非線性、非平衡、突變、分叉、混沌、路徑依賴等等,有其非常的普適性。即在某一特定研究對象上所獲得的某些概念和規律,常常可以在一些其它的研究領域再次實現。非線性現象的一些基本特征,可以在各種具體復雜系統中以各自的方式展現出來,非洲白蟻作窩過程的非線性生態行為,竟與單模激光的基本模式是一致的。這種非線性現象的普適性,是學科交叉可以獲得實質性進展的重要基礎。”
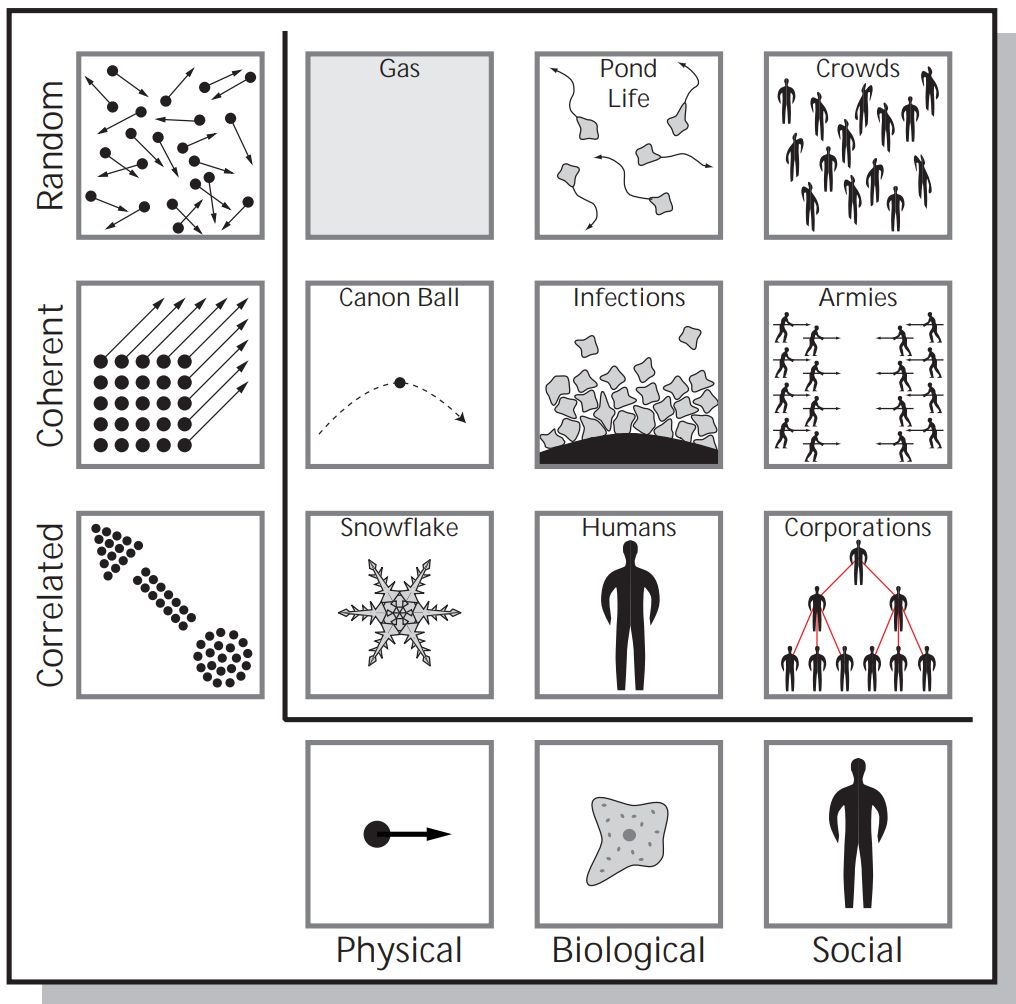
圖 1. 三種系統。
圖上每列包含 3 個示例,都是由相同組元構成的系統(從左到右的基本組元分別是:分子、細胞、人)。但系統中組元的關系不同,最上面是隨機(random)系統,每個組元的行為都獨立于所有其他組元的行為。下面是相干(coherent)系統,所有組元表現出相同的行為;例如,某部分的行為(例如炮彈的位置,方向和速度)完全決定了其他組元的行為。最下面的相關(correlated)系統介于上面兩個極端之間,系統各組元的行為確實相互依賴,但又沒有那么強烈,以至于每個組元都以相同的方式起作用。例如,一片雪花某部分的形狀會和另外部分的形狀相關,但不會完全決定另外部分的形狀。
B. 什么是復雜度 (What is complexity)
行為的復雜度可以用描述這個行為的信息長度(length of its description)來表示,這個長度取決于系統可能的狀態數量。例如一個電燈只有兩種可能狀態——開或者關,這只需要 1 個比特長度的信息就可以表示出來(0 或者 1)。而 2 個比特長度的信息可以用來表示 4 種可能行為,分別是 00、01、10 和 11。同樣的,可以用 3 個比特的信息來區分 8 種行為。復雜度可以簡單表示為 C=log2 (N),其中N為可能行為的數量。嚴格的說,這個公式是給出了一個關于復雜度的上界,如果一個系統中各個行為出現的概率不一致,則可以通過用較短的長度來描述常見的行為,用較長的長度描述小概率行為來降低平均描述長度。在這兒,最重要的是:可能的系統行為數量越多,系統的復雜度越大(the greater the number of possible behaviors, the greater the complexity)。
定義可能的行為空間要非常小心,根據不同的要求形成的可能的行為空間是不同的。比如,如果只關心燈泡的明暗,就只有兩種可能性,但如果關心制作一個燈泡的復雜度,則要考慮到燈泡各個組成部分如何安排在一起,行為空間就要大很多[3]。另一個例子,讓一個計算機程序正確地解決一個 4 項的選擇題,看起來用兩個比特就可以搞定(可以描述 4 種選擇),但這樣的計算機編程實際難度是很大的。這種困難是因為我們并不能預先知道會有些什么題目,而希望計算機程序能對任意多項選擇題進行正確回答。只有考慮大量的可能情形,計算機程序才可能對任意的多項選擇序列給出正確反應。
[3]譯者注:復雜度是相對的,同一個系統在不同尺度上的復雜度不同。補充一個例子,對于普通人,如果他/她只關心電視機是否能看,電視機就只有正常和不正常兩個狀態。但對于電器修理工,就必須弄清里面的電子元器件間的相互配合,會有更多的狀態——例如不同的元器件損壞了。對于后者,這個電視機的復雜度更大。
C. 什么是復雜系統(What is a complex system)
一個人體和一個由相同分子構成的氣體系統,哪個更加復雜?后者具有更多可能的分子排列組合,所以具有更大的復雜度和更大的熵或者無序度(disorder),這是因為構成人體的分子不能隨機排列組合,但氣體系統中的分子可以。但我們在討論復雜系統的時候,我們會選擇有特定分子排列順序的人體而不是氣體來進行研究。植物、城市都可能是復雜系統科學討論的對象,這些對象看起來是更加有序、熵更低。是否低熵的系統就是復雜系統?并不是這樣的!無序程度最低的時候,系統中所有組元具有同樣的行為(像圖1 所提及的相干系統一樣),我們直覺上也不會認可這是復雜系統。看起來這兒存在矛盾,解決這個矛盾的關鍵是明白系統描述的長度取決于用來描述它的細節的層次。復雜度依賴于尺度 (scale)。在微觀狀態,氣體比人體復雜,描述氣體中所有分子的位置和速度要比描述人體中所有分子的位置和速度更加困難。但在人類的感知層次,人類只能感受到氣體宏觀一些的行為,如溫度和壓強。相反,在這個層次上,人體的行為更為復雜,他們有各種活動或運動形式,還有喜怒哀樂的情感。在人類感知的層次,氣體是非常簡單的,因為只有涉及數萬億規模的分子行為才能被人感知,而對于這種規模的氣體分子人類感知可以區分的行為種類沒有多少。熵只是對于最微觀層次上復雜度的度量,但對一個系統的刻畫(characterizing)需要在多個尺度上理解系統的復雜性。圖2描繪了一些系統的復雜性曲線(complexity profile),系統復雜度是尺度(規模)的函數,行為的尺度(規模)等于系統中的耦合相關的組元數量。
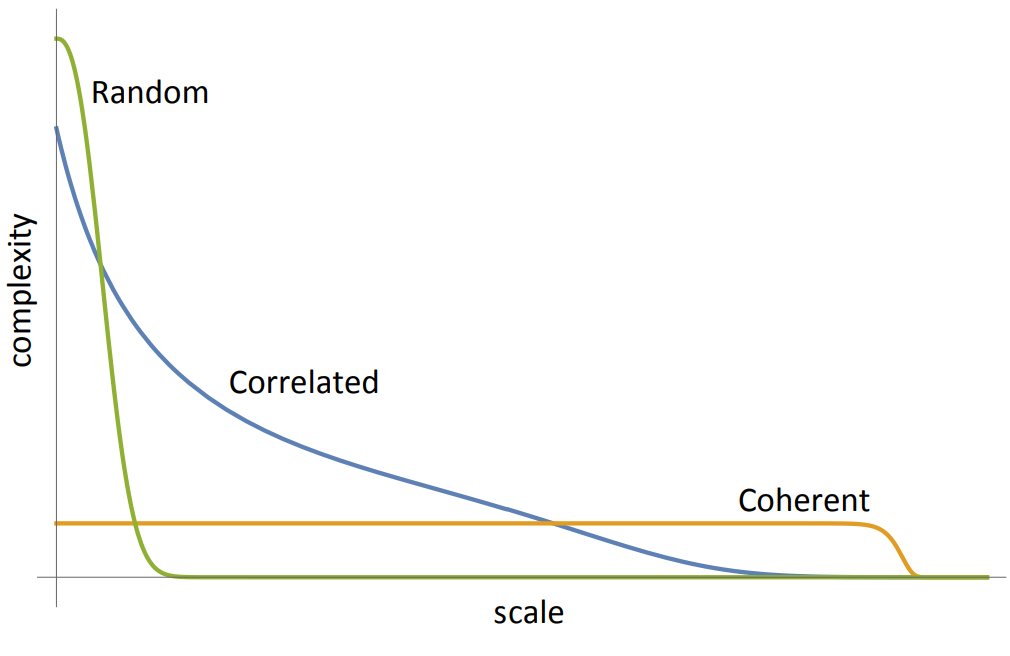
圖 2. 隨機、相關和相干系統的復雜度曲線。
隨機系統在微觀小尺度上具有大復雜度,在宏觀大尺度上復雜度低。相干系統的復雜度不會隨著觀察的層次發生變化。相關系統介于二者之間。所有復雜度隨著尺度的減少有增加的趨勢。
如圖所示,隨機 (random) 系統在最小尺度上很復雜,但尺度升高時復雜度迅速降低。而相干 (coherent) 系統在不同尺度上的復雜度保持不變,例如一個炮彈的運行速度和炮彈上的所有原子的運行速度是一致的,而整體的位置和所有原子的位置也是相對固定的。相關 (correlated) 系統介于二者之間,在不同的尺度上會有不同的行為。例如,遠遠地勉強才能看清的一個人,談不上什么復雜程度,但如果越靠近細節會逐步增加,首先會有其位置和速度信息,然后有四肢的信息,然后有語言、面部表情、手指的細微動作等,尺度再小就會到達 DNA 和蛋白質層次,最后到達單個的原子和分子層次,隨著觀察或研究的層次越細微,“人” 這個系統的復雜程度會逐步增加。復雜度和尺度是相關的,隨著尺度的變化,系統的復雜度會發生變化。對同一個系統來講,層次越低尺度越小時,系統的復雜度越高[4]。復雜度會隨著觀察尺度發生變化,往往呈現遞減(或不變)的函數形式。在 s 尺度上系統的復雜度可定義為:
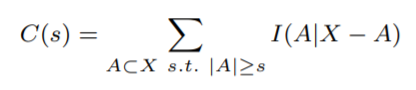
其中 A 表示這個尺度及以上的所有可能子集,I(A|B) 表示 B 條件下 A 集合中所有隨機變量的多變量互信息 (multivariate mutual information)。
[4]譯者注:前面提到的電器修理工觀察電視機的尺度或者層次就要比使用者觀察的層次低,修理工除了判斷電視機能否工作外,還要了解更多的電視機元件的細節,因此,對于修理工,電視機有更大的復雜度。
D. 復雜度和尺度上的此消彼長(tradeoffs between complexity and scale)
復雜性需要序(order),復雜系統的形成確實涉及熵的降低,需要降低系統在小尺度上的復雜度。即要獲得高尺度上的復雜性(增加復雜度),系統中的微觀個體必須有一定的關聯,這種微觀關聯會降低系統在低尺度上的復雜性(減少復雜度)。更精確地講,對于固定組元集合及個體可能行為集合的系統,復雜度與尺度的關系曲線下方的面積是一定的,因為這個面積與組元的相互作用無關。需要注意的是,有時候引入系統組元之間的交互可能會改變系統組元的行為種類,從而使曲線下面的面積增加。例如當系統中的兩個人進入交談,這能反映出兩個人的關系,而交談也是一個新的原先沒有考慮的個體行為。
考慮一個有一些工人的工廠,可以將一個有很多工人的工廠在一定的時間內生產的同類產品的數量作為尺度(規模)的表示;而在要求的尺度(規模)條件下,工廠能夠生產的產品類型的數量可以作為工廠的復雜度。這兒的規模和復雜度是緊密相關的,要想生產大規模的同類產品,就需要很多工人同時進行同樣的工作,從而減少復雜度;反之,只有在工人具有較高的獨立性時,才有機會創造出更多類型的產品,但此時就不能在產品的數量上有高的要求。當然,可以通過增加機器和工人使工廠在復雜度和規模上都有所提高,但當工人和機器的數量一定時,就只能追求其中的一個:要么規模要么復雜度,它們中的一個增加時另一個就會減小,如圖3所示[5]。
[5]譯者注:一個學者的精力總量是有限的,他/她可以廣泛涉獵不同的領域,但容易淺嘗輒止,很難在某一個領域獲得深入的洞察;他/她也可以長期在一個具體領域鉆研,由一系列內容相關逐步深入的文章形成豐碩的成果集。
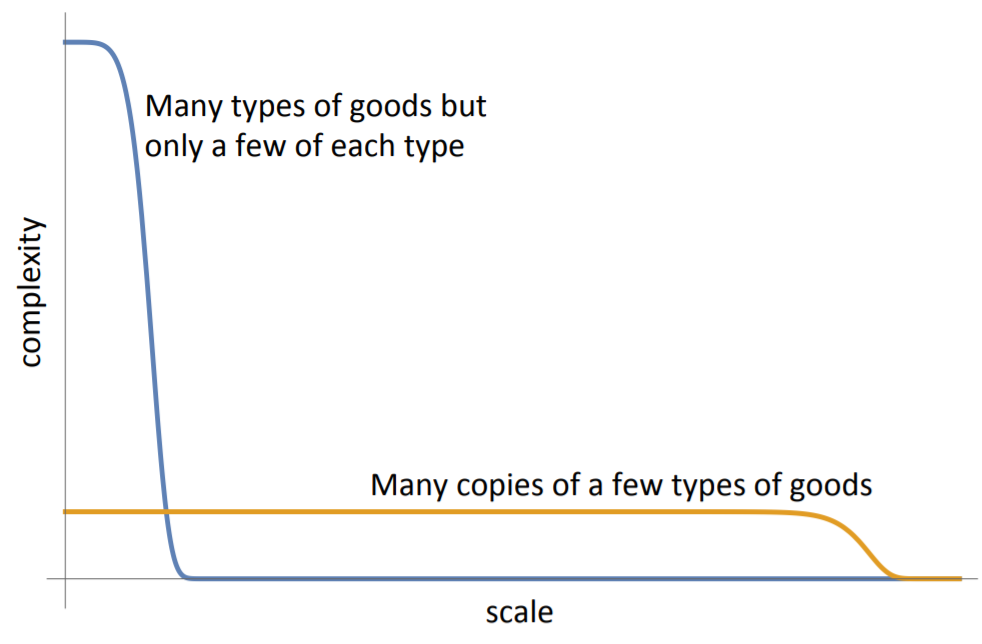
圖 3. 工廠的復雜度曲線。
可以選擇產品種類少,但數量大的生產方式;也可以選擇數量少但種類多的生產方式。前者是大規模(尺度)小復雜度,后者是小規模(尺度)大復雜度。
對復雜度和規模的抉擇實際上是對適應(adaptive)還是效率(effective)的抉擇。復雜度越高,個體行為相對獨立,具有更多的行為方式,整個系統會有更大的適應性;反之,若系統中的很多個體都進行高度協作,可以高效率完成既定任務,滿足大規模或者大尺度上的要求,但這種有效系統對于自身或者環境未來不確定變化的適應能力會降低。設計一個可以應付所有可能沖擊的高適應性系統,一定是以犧牲系統的某些大尺度功能為代價的。前蘇聯的人們相信他們的經濟將超過資本主義經濟,因為資本主義國家經濟體有過多浪費,例如很多企業會因為做同樣的事情而存在相互競爭,而讓經濟體中的每個人都協作起來會讓經濟運作會更加有效。確實如此!但構建大規模的經濟結構是以犧牲低尺度(規模)的復雜性為代價的,結果就喪失了適應性,這種經濟體面對多變環境的新情況會缺乏應變能力。當然,監管不當的資本主義經濟,也可能會因為市場力量的過于集中、有害反饋環的存在或者個體的從眾行為而變得適應性不良。
無論市場、政府還是其他系統,想要提高其在大尺度上的復雜度,就必須減小其中組成個體的復雜度。但很多時候,以小尺度部分個體的自由為代價,而換取大尺度(規模)上的合作,可能是非常值得的。
E. 為什么要復雜(Why be complex)
必要多樣性法則 (Law of Requisite Variety) 要求,為了保證有效性,系統必須足夠“復雜”得和環境一樣,這樣系統才能對于環境的交互進行合適的應答。若環境有 100 種不同行為需要應答,一個系統如果能對這些不同行為都給予不同的反應,那么這個系統就是有效的;但如果系統只有 10 種可能行為,那么這個系統對于環境而言是無效的[6]。
[6]譯者注:極端一點,如果一個系統對于外界所有輸入都只有一種應答方式,說明系統的功能完全喪失,這個系統也就是徹底無效的。在有效的對話時,一方的提問總能獲得對方合理的應答,問題多樣性大于回答多樣性的時候就會顯得回答者沒有認真應對或者沒有能力應對。
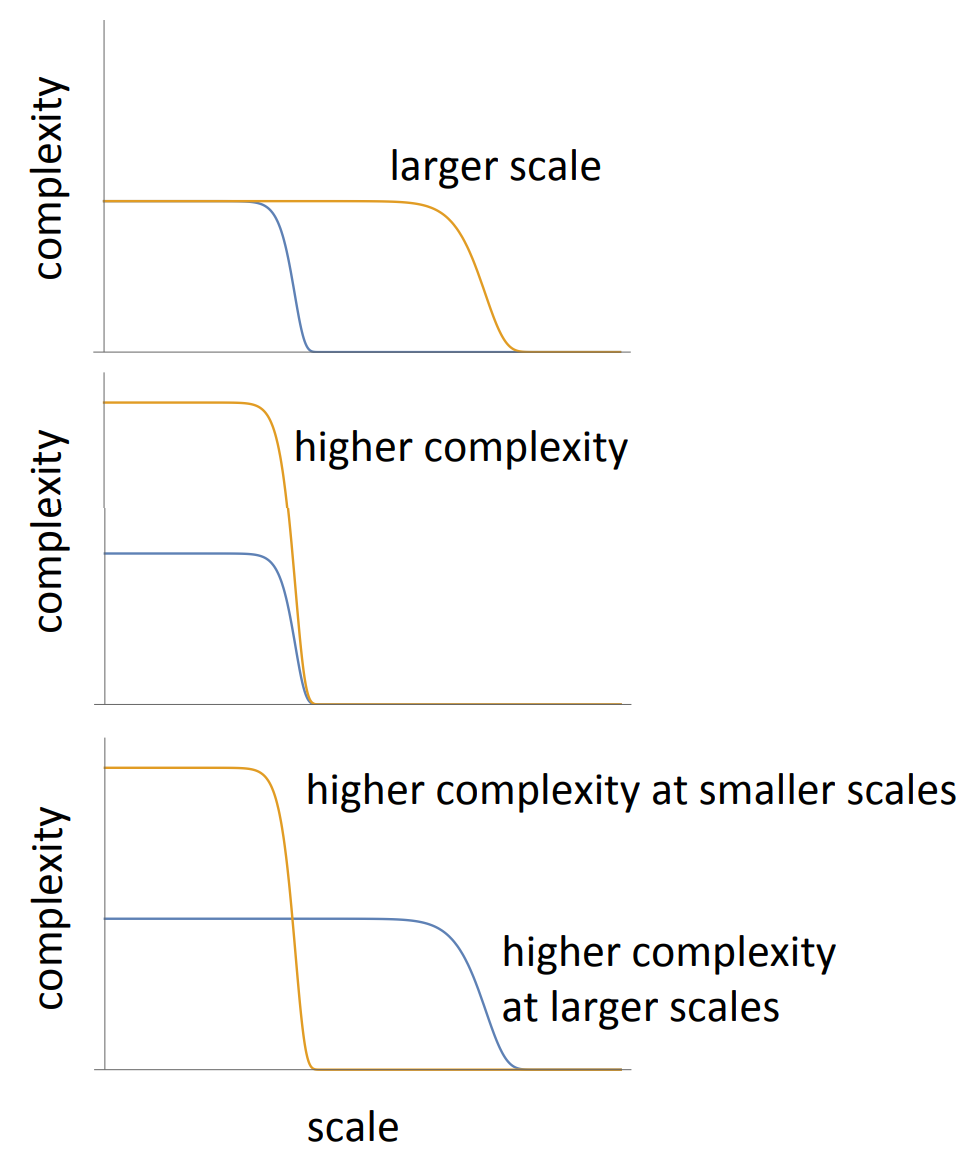
圖 4. 沖突中的兩只軍隊的復雜度曲線示意圖。
頂部:如果兩支軍隊具有同樣的可能行為,復雜度一樣,但規模(尺度)不同,規模更大的一方更有優勢。中:如果兩支軍隊規模相同,但可能的行為數量不同,后者更有優勢,因為其復雜度更高。下:如果有兩支軍隊以不同的規模和行為數量運行,哪一方占優勢很大程度取決于具體作戰時的地形。例如在廣闊平坦的地面或者在山區叢林地帶會有不一樣的結果。
前文提到,復雜度必須定義在一定的尺度之上,所以我們要完善這個必要多樣性法則:為了保證有效性,系統必須匹配它與環境在所有行為交互尺度上的復雜度。如圖4,討論兩支作戰的軍隊,任何一方都可以將自己作為系統,而將對方作為需要應答的環境的一部分。如果兩支具有相同的行為數量,即具有相同的復雜度,如果某一個具有更大的尺度(都是嚴格控制的軍隊,其中一個規模比較大),規模大的軍隊獲勝的可能性大一些。如果這兩支軍隊的規模一樣,但復雜度不一樣(如兩個規模和武力強度一樣的艦隊,一方比另外一方機動性能更好),高復雜度的軍隊取勝的可能性更大,因為高復雜度軍隊可以針對低復雜度軍隊的不同行為采取不同的動作,但反過來不行。但若兩軍情況像圖4中最下面子圖所描述的,一個是大規模小復雜度,一個是大復雜度小規模,其作戰的結果就會取決于具體的地形(此時尺度或規模將被限定):在廣闊平坦的地方,高尺度高復雜度的軍隊更可能獲得勝利,若在山區叢林,在尺度小情況下具有高復雜度的軍隊大概率會贏。美軍和越南游擊隊,前蘇聯軍隊和阿富汗游擊隊就是非常好的例子。
有另一個有意思的例子,人類的健康醫療體系往往會包括這兩種不同的任務:個案治療——對于不同個體不同的疾病具體處理,具有小尺度(規模)但高復雜度特征;而接種免疫——對所有的人采用同樣的處理方式,具有大規模低復雜度的特征[7]。
[7]譯者注:各個國家的教育也具有這樣的特征,書籍和電視傳媒提供了大尺度低復雜度的教育方式,家教或者其他一對一培訓等提供了最低尺度最大靈活度的教育方式,學校則在中間尺度上提供了中間復雜度的教育。
歐元區的境況提供了一個多尺度復雜度不匹配的可能例證。在這個區域,財政政策的制定主要在單個國家和地區進行的,因此在國家范圍內具有更高的復雜度但在整個歐元區尺度上的復雜度相對較小,而貨幣政策的制定尺度就在整個歐元區,因此在整個歐元區這個大尺度上有較好的復雜度,但它會缺乏在各個國家/地區這個小尺度上變化的能力(即缺乏小尺度復雜性)。許多人認為歐元區的經濟發展遇阻,就是因為這種不匹配阻礙了財政政策與貨幣政策之間有效的交互作用。
實際問題處理時是很難做精確討論的,因為精確地估計尺度和復雜度是難以做到的,所以復雜度隨著尺度變化的曲線基本上不能準確地描繪出來,但近似的有關復雜度不匹配的分析還是可以做的。正如即使在系統的精確機制和結果存在不確定性時也可以使用這種對可能行為空間的分析一樣,物理學家可以利用熵的性質(有時考慮與熵有關的量如何在整個尺度上變化)對相變進行分類。即使它們無法根據第一原理確定精確的數量,例如相變所產生的熱量或發生的溫度。只是如果要討論如何糾正具體的不匹配問題,還是需要更細節的分析。
無論在什么尺度上討論,復雜度的大小本質上沒有好壞。只是如果要執行的任務的復雜度與執行該任務系統的復雜度不匹配時,就有問題了。尤其要注意,某種情況下的系統又可能是另外情況下的一個任務或者環境,這樣,一種幫助某個系統與其環境進行交互的復雜度可能會阻止其他系統的有效管理。順帶一提,人類的情感特點似乎反映了這一原理:當我們所處的環境過于簡單時,我們會感到無聊;若環境太復雜了,我們又會感覺不知所措。
F. 分塊的系統(Subdivided system)
即使在當系統的復雜度和環境的復雜度一致的情況下,仍可能存在復雜度不匹配的問題。舉一個例子,一個系統有四個人,他們每個人能搬動 100 斤的物體,假設每一對中的兩個人會一起協調一致干活而組成兩個朋友對。若當前任務是搬走兩個各 200 斤的沙發,這個任務是能被完成的,因為這個 4 人系統在適當的尺度下具有足夠的復雜度,每對朋友一起搬一個沙發就能完成任務。但如果讓每對朋友中的人被安排去搬不同的沙發,這個時候搬同一個沙發的就不是一對協作的朋友,按我們的假設不是朋友的人不能協作,那他們就搬不動沙發了。這個任務失敗的原因是雖然兩對朋友的系統具有搬動兩個沙發的復雜度,但朋友系統的某一種劃分與自然的沙發系統的劃分是不匹配的。這種不匹配可以這樣看,某個沙發需要 200 斤的協作能力,但這兩個人分別提供了 100 斤的能力。學術部門的組織可以提供一個更好的劃分不匹配(subdivision mismatch)的例子。當前,為了組織知識和協調人員,學術界形成了多層的分塊結構,包括各個部類、子領域等,整個學術界在多個尺度上都有足夠的復雜性(這個尺度可以用協調的人員數量或者知識的量表示)。但學術界需要處理的學術問題集合存在一個自然的細分。如果這兩種細分不同,即使學術界在多個尺度上能保證了復雜性要求,但沒有辦法解決看起來應該可以解決的學術問題。最近幾十年交叉學科中心和計劃的興起,表明人們已經察覺到這種不匹配,但整個學術體系的結構(包括學生的培訓方式,學術成果的發表等)仍可能會阻礙一些沒有完全屬于某個學科或子學科的科學問題的研究進展。
以上示例說明了這個原理——為了使系統對其環境的某些行為集做出不同反應,不僅要在整個系統的各個尺度上和環境行為各個尺度的復雜度相匹配,而且系統的每個子集的復雜度也要和環境所對應的子集在所有尺度上都能匹配。這種匹配要求前者至少具有和后者相同的復雜度。應用此方法的良好經驗法則如下:有關系統獨立部分的決策可以獨立做出,而相關聯的部分則需要相關聯地制定。因此,做出此類決策的組織應進行相應劃分,以便其劃分與它們相互作用的環境的自然劃分相匹配。在人類大腦中是存在這種分塊的,一些神經網絡也采用分塊的形式研究。一些文獻研究表明,系統采取分塊的方式匹配環境的自然劃分要比采用增加內部交互作用的方式要獲得更好的效果[8]。
[8]譯者注:對資源的管理,包括人力資源和物質資源,其中最重要的是要素的優化配置,這個配置實際上也是對于自然任務劃分的合理應對。為滿足不同業務的需求,有效的公司進行合理的部門調整以積極應對。
G. 層級性(Hierarchies)
系統的一般組織方式是通過控制其層次結構。在一種理想化的系統層次結構中,沒有橫向連接,涉及層級結構多個組元的決策都必須通過一個公共節點,其他組元都(直接或間接)在這個節點的管轄下。如圖5所示,這種層次結構系統的復雜度曲線取決于控制結構的緊性程度(rigidity)。
一個極端情況是,任何決定(無論大小)都由層次結構的頂部做出。這種結構在不同尺度(層級)上會具有同樣的復雜性,因為所有的決定都是同樣的人做出的,具有同樣的可能應對方式。另一種極端是層次結構中的所有個體在此結構中沒有信息溝通,自行決策,此時整個結構的復雜性比個體層次的復雜性高不了多少。一般的層次結構都是介于這兩種極端之間,不同的決策是分別在不同的層級做出的。
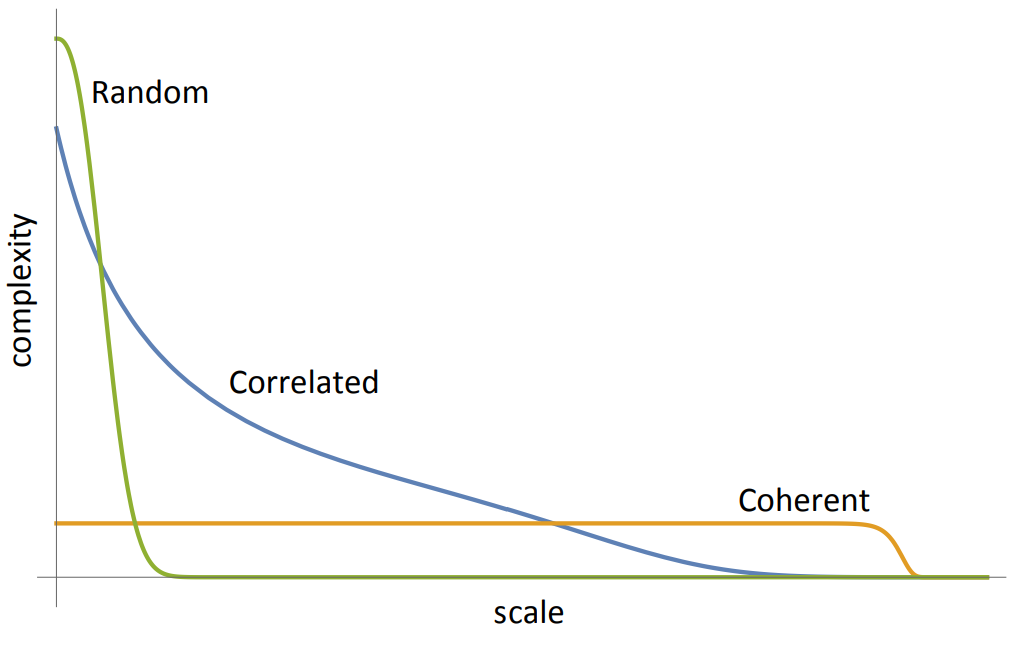
圖 5. 兩種層次結構的復雜度曲線。
每個層次結構的總人數相同。在這里,尺度由協調的工時表示。在一個層次結構中,所有決策,無論規模如何,都是由一個人決定;在另一種層次結構中,不同的決策在結構中的不同層次做出。
沒有天生就優異的層次結構類型。對于一種具體的環境,最好的層次結構是它的復雜度構型可以和需要其完成的任務復雜度相匹配。緊控制這種頂層決定(top-heavy)的層次結構不適合這種底層具有很多變動需要應對的環境狀況。同樣,松控制(loose control)的層次結構也不適合處理需要大尺度(規模)處理應答的環境。例如,美國政府系統具有較強的中心化特征,相對地方的州政府,聯邦政府的權力很大。這種層次結構無法在小尺度上具有充分的復雜度來匹配和應對地方性的變動。但反過來,一個去中心化的系統無法保證在大尺度(規模)上具有足夠的復雜度來很好地處理國家層級的問題和應對方案。將決策權賦予層次結構的高層可以提高尺度(規模)和有效性,但會減少適應性,因為這種情況下一旦決策是錯的,影響巨大,恢復也更為困難。我們不僅要考慮政府整體的復雜性匹配,同樣還要考慮到施政系統的子劃分(結構)以適應環境的自然劃分。在同樣的州,美國的城市區域在某些方面彼此較為相似,但它們和鄉村的差異很大。所以,將美國劃分為 50 個州,確實提供了低尺度(規模)管理的復雜性,但這種復雜性對于自然的城市-鄉村劃分還不夠,而這種不匹配會導致州層次上的一些問題。更好的方式應該是在更低的層次,例如允許城市和鄉村可以有不一樣的政策。類似的,也有人認為聯邦政府應該將一些權力轉移給州政府。
很有必要區分清楚層次的復雜度和層次中的人能做的決策的復雜度。例如,可以設計一個緊控制的層次結構,該層次結構可以進行大量的大尺度(規模)行為的可能,即在最高層次上具有高復雜度,但要知道即使是最有才能的人,他或她的決策能力也是有限的,從而頂部的個人可能因為缺乏足夠的復雜度來做出正確的決定。這種不匹配就會導致層次結構的一個重要局限:層次系統最大尺度上的復雜度可以決定整個組織的行為,但這又取決于層次結構中頂層的一部分人的能力(復雜度)。因此,當將最大尺度(規模)的行為被要求匹配的復雜度超過試圖進行監管的個人或委員會可實現的決策復雜度時,這樣的層次結構必定會失敗。指令性經濟(command economies)的失敗就是一個這樣的例子:整個國家的資源和勞動力的優化配置是一個非常復雜的問題,是任何個人或團體來他們難以完全弄清并給出正確指令的。而市場經濟不同,市場不是通過個人而是通過網絡化的系統來分配資源,這種決策類似于人腦做出決策,但它并不是基于任何神經元的功能。要注意,系統為應對環境行為的決策任務的復雜度通常遠大于系統或環境單獨存在時的復雜性。例如,如果系統和環境都具有 10 種可能的行為,則系統具有足夠的復雜度以匹配環境,這樣的對應方式總數有 3,628,800(10 的階乘)種。但系統適當的決策行為需要對應到具體的環境條件,就是要從 3,628,800 種可能性挑出一個正確的。這說明,系統及其環境的可能行為空間可能要比有關系統行為和環境管理的可能決策空間要小很多。
我們先前考慮了只有垂直連接的一種理想的層次結構,若加入橫向連接則可以提供另一種讓系統實現更大尺度(規模)行為的機制。例如,讓城市之間相互交流要比它們只與州和中央政府互動更好,它們可以相互借鑒好的政策,還可以基于其他城市的錯誤教訓預防自己的錯誤。通過這種我們下面會提到的進化過程,所得到的大尺度(規模)的決策行為(如某一個政策可能被多個城市采用)要比任何個體單元做出的決策都要更加復雜。這樣的橫向連接也可以引入到一個頂層(如中央政府)保持重要控制權的層次系統中。更進一步,我們還可以考慮可以改變權重的橫向連接,但要注意,過強的橫向連接會導致微觀個體們出現類似羊群效應的行為,使得系統小尺度上的多樣性不足;而過弱的橫向連接會導致個體合作的不足,從而影響大尺度上的功能實現(依賴于復雜度)。
第二部分、分析復雜系統 (ANALYZING COMPLEX SYSTEMS)
前面已經介紹了具有多組元的系統的一些一般特征,本部分試圖回答這些問題:
1 我們如何研究具體系統?
2 我們如何分析復雜系統中的數據?
3 我們應該選擇什么樣的數據研究?
A. 我們如何理解系統(How do we understand any system)
即使是非常簡單的機械系統也具有數萬億個分子,但令人吃驚的是我們仍然可以很好地理解一些宏觀系統,因為這種系統具有“尺度分離”(separation of scales) 的特性。如圖6,我們感興趣的系統行為發生在很高的尺度上,遠離單個分子行為的尺度,而中間尺度沒有什么行為。這種分離讓我們可以分別討論系統的微觀層次和宏觀層次,例如對于機械系統,在宏觀上我們用牛頓力學來分析它,在微觀上用熱力學來進行討論。
更一般的講,上面說的方法是一種平均場理論(mean-field theory)。在這種理論中,系統組元的平均行為被建模,而單個組元對于平均行為的偏差被視作相互統計獨立的隨機變動(statistically independent random fluctuations)。這種方法非常適用于計算機、汽車、飛機和建筑物等系統的研究,因為各個分子的運動除了一些主要不相關的波動外,剩下的部分可以很好地用它們所在的部件整體的運動來描述。人們在分析生物、社會和經濟系統時也經常采用這種方法。這種獨立的隨機性假設在許多情況下都適用,但并不總是適用于復雜系統。所以,弄清楚使用平均場的條件尤為重要。
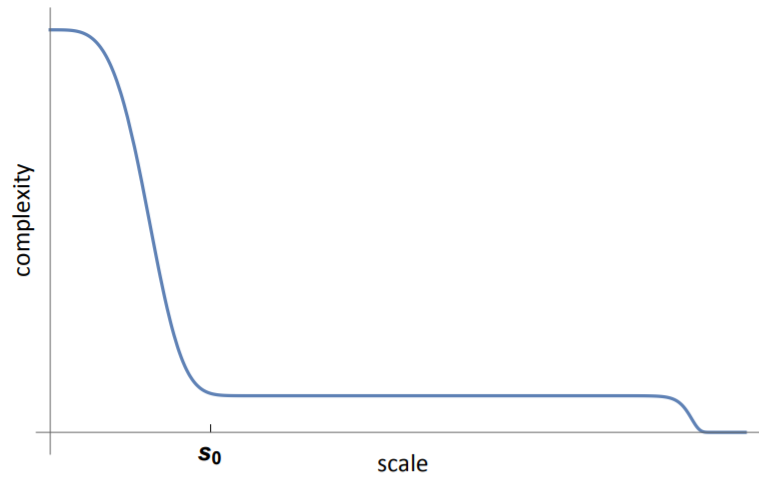
圖 6. 具有尺度分離特征的復雜度曲線。
尺度分離要求發生在特征尺度 s0 之下的行為基本獨立,這樣它們的行為的平均效果才是和大尺度有關的。
B. 什么時候平均場理論失效(When mean-field theory breaks down)
平均場理論能分析的系統所呈現的大尺度行為是其組元行為的平均效果。這種系統必須滿足尺度分離特性,而尺度分離要求系統在一定尺度(規模)之上看低尺度組元的變動在統計上要近似獨立。需要強調的是,即使對于組元具有很強相互作用的系統,只要這種作用能反應在系統的平均行為上,平均場理論仍然是適用的。此時,系統的每個組元被建模,就像它們是在與系統的平均相互作用一樣(系統的平均就是平均場)。例如,平均場理論可以很好地描述了固體在大尺度上的運動,雖然在固體中分子之間的相互作用非常強,但這種作用的效果只是用來保持了每個分子與平均位置(質心)的距離和方向。在一些情況下,對于經濟市場的建模可以考慮每個市場參與者與市場平均的供需合力的作用,而不必考慮所有參與者之間的相互作用。
當系統中的組元之間有足夠強的關聯,或者說系統中的某個組元與其他的一些特定組元的相互作用不能被忽視(與這個組元和系統其它部分的一般交互非常不一樣)的情況下,平均場理論就會失效。這個時候,系統的大尺度行為不僅僅由系統各個組元的特征決定,還取決于組元之間的相互關系。例如肌肉整體的行為可以大致由單個肌細胞的行為大致了解,但人類大腦的行為相對單個神經元的行為有根本性的偏離,因為認知行為主要決定于神經元之間突觸連接的變化。同樣,森林的復雜生態行為并不是由各個分離的組成生物的行為所確定的。順便說一句,平均場理論無法描述某些物理相變(phase transitions),導致物理學家開發出重整化群(renormalization group)這樣的新的多尺度研究方法,可以作為許多復雜系統科學研究的基礎工具。
在小尺度的隨機現象不滿足統計獨立性時,復雜系統往往在大尺度上表現出平均場理論所不能解釋的波動或偏離(?uctuations)現象,如森林火災、社交媒體上流傳甚廣的虛假消息和經濟市場的崩潰等。在有些時候,這些大波動是為了適應性,它們讓系統對于微小的輸入產生集體反應。例如,人體對于空氣密度一種小擾動會有強烈的反應,就是當他/她聽到自己的名字時。但要提防的是,這種大尺度(規模)上的波動有時會造成系統性風險[9]。
[9]譯者注:銀行之間的借貸網絡可以有效地進行金融資源的優化配置,低成本快速應對環境的變化,但這種網絡連接也是出現系統性金融風險的基礎。
C. 肥尾分布及及系統風險(Fat-tailed distributions and systemic risk)
當系統的組元在某個尺度之上表現相互獨立時,系統在大尺度上的波動幅度會呈現鐘形的正態分布特征,這是中心極限定理所保證的。此時,系統的大尺度行為會有明確的均值和標準差,偏離均值幾個標準差之外的事件極不可能發生(astronomically improbable)。但若組元相互關聯,就可能導致另外一種分布,在這種情況下,一些極端事件(extreme event)雖然發生的概率還是比較小,但要比正態分布所預測的要大得多。這種分布被稱為肥尾分布(或厚尾分布),如圖7所示。例如,某個地區成年男性的身高服從正態分布,統計發現最高的人的身高也不會有平均身高的 2 倍那么大;但財富分布就不一樣,它具有肥尾特征,你會發現很多人擁有的財富超過平均值的 1 萬倍以上[10]。
[10]譯者注:有一個簡單的貨幣轉移模型揭示了財富分布的冪律機制——當個體有隨機儲蓄率的時候,通過個體之間貨幣的隨機交換,得到財富分布的冪律分布。在模型中,貨幣在個體轉移使得個體的財富并不是獨立的,而是具有廣泛的關聯特征。
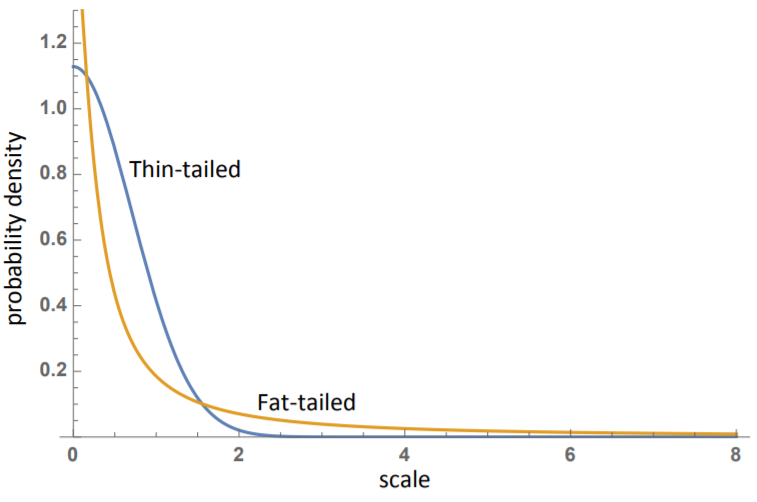
圖 7. 正態分布(細尾)和冪律衰減分布(胖尾)。
胖尾分布可能看起來更穩定,因為小尺度(規模)波動的概率更小,應該不容易產生極端事件。而實際上,胖尾分布可以有相對交大的概率產生極端事件的,即使這種事件在正態分布的情況下可能要等上幾萬倍的宇宙壽命才可能發生。注意,該圖的軸是被截斷了的,圖示的肥尾分布可以很小的但不可忽略的概率(0.04%)到在 100 萬或者更高的尺度(規模)的地方發生事件。
組元的相互依賴可能會使系統看起來更穩定,因為它可以減少小尺度波動的程度,但也不完全是這個樣子。舉一個例子,想象一下 我們有100 個梯子,每個梯子都有 1/10 滑倒的可能性。如果梯子彼此獨立,則所有梯子滑倒的概率會極其低,這個概率要比從宇宙中所有原子中隨機選擇一個剛好選出特定原子的概率的 1020 分之一倍還小。如果我們把所有梯子綁在一起,從某種意義上講,我們將使它們更安全,因為任何單個梯子滑倒的可能性都會比單獨使用小得多。但我們若真的把它們綁在一起,也將使所有梯子一起倒下的可能性變得不可忽視。其他還有一些例子,如金融系統的相互關聯導致全球市場崩潰的可能性,出行路線的連接增加了傳染病爆發的可能性(如西班牙流感)。一般而言,當某個事件發生的概率具有胖尾分布特征時,標準的統計方法往往會失效,胖尾分布會導致人們嚴重低估極端事件發生的可能性。要知道,一些胖尾分布的期望和方差可能都不存在,即使存在,通過有限的數據也難以獲得可靠估計[11]。
[11]譯者注:無論數據多少,從觀測數據來估計的均值和方差一定是有限的,對于期望和方差無限的理論分布來講,這種估計一定是偏小的。
D. 理解復雜系統(Understanding complex systems)
實證研究復雜系統失敗的主要原因有如下幾點:(1)通常收集系統組元的數據要比收集組元之間交互作用的數據要更加容易。如果沒有捕獲到與復雜系統的有關信息就會造成實證工作的失敗,因為復雜的大尺度行為嚴重依賴于此類交互。(2)不適當的數據分析可能嚴重低估極端事件的可能性(尾部風險)。
(3)一些實證分析通常采用線性(linearity)假設,即假設一組因素的總影響等于單個因素影響的和,但非線性作用恰恰是復雜系統的一個重要特點。
如果常用的標準方法不適用,我們該如何來理解復雜系統?我們對于所有這種具有許多組元系統的理解依賴于普適性,即系統存在不依賴于微觀細節的大尺度行為。基于組元之間足夠獨立的假設,通過平均場理論討論系統的大尺度行為而無需考慮到系統的所有細節(在一定尺度之上,組元的變動必須具有足夠的獨立性,以滿足中心極限定理的要求)。另外要注意平均場理論只是普適性的一個例子。
聲音是另一個例子。所有材料,無論它們的成分,都可以傳播聲波,而且聲音在所有材料中的行為都非常相似。這是因為在與聲波相關的長度范疇(length scale)遠遠大于介質中單個原子或者分子的大小,原子和分子尺度上的微觀參數只會影響聲音的速度。要注意,聲波不能通過系統平均行為的某個屬性來理解,如材料的平均密度,而恰恰是密度對平均偏差的系統關聯形成了聲音。人類也無法通過關注原子運動這樣的小尺度細節來理解聲音。實際上,科學家對聲音的理解是在了解原子是什么之前。理解聲波的關鍵是要認識到它們具有多尺度結構——對應于較低頻率的較大尺度(幅度)波動和對應于較高頻率的較小尺度(幅度)波動,再對他們進行相應的建模。
Lim 等人將這種方法用于研究種族之間的暴力沖突(圖8)。他們建立了一個預測模型來分析種族暴力可能在何處發生,并將其模型應用于解釋發生在印度和南斯拉夫的實際現象。種族暴力有多種原因,如文化依賴機制或包括人口統計或經濟統計特征的區域平均屬性等,但作者關注了種族在地理分布上的多尺度格局(multiscale patterns)。他們發現當多個種族比較好地混合在一起時,或者隔離得比較好時候,都不會發生種族暴力。種族暴力只在不同的種族人群被分開放入一些地理區片的情況下(類似于水和油的混合)才會發生,而且沖突發生的可能性和區片的大小有密切的關系。當然,兩個種族之間的仇恨既可能是這種地理混據的原因,又可能是地理混據的結果。文章的研究表明通過設定合適的邊界可以有效預防種族沖突(就像另一篇文章提到的瑞士當前的一些自然和非自然的政治邊界的作用那樣)。
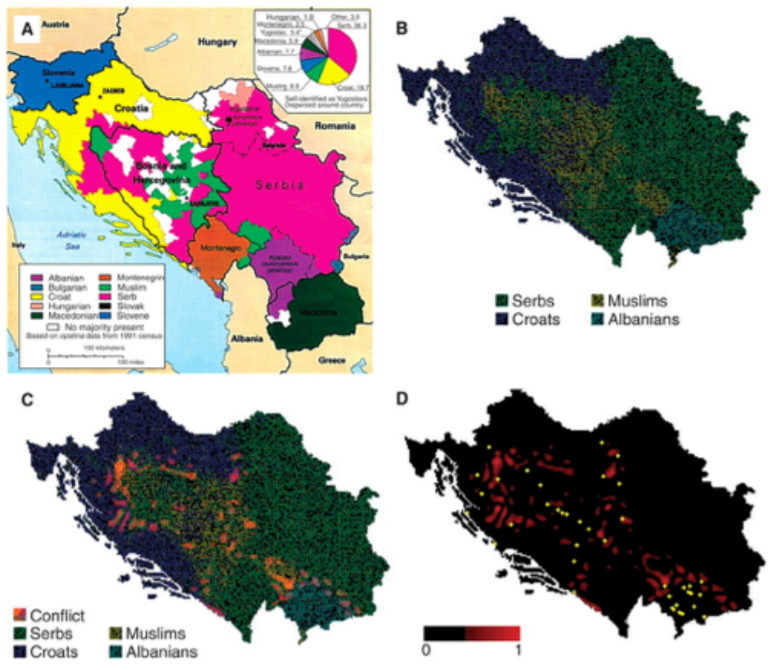
圖 8. 暴力沖突地點預測。
A 為問題背景;B 為不同種族分布的地理格局;C 和 D 中的紅色是他們的模型預測了潛力的暴力沖突點;D 中黃色的點是歷史上有過報道的被證實的點。
弄清楚任何一個復雜系統的所有細節都是不可能的,大多數系統具有尺度分離特性,系統在小尺度上具有很高的復雜度。但不同于普通的具有尺度分離的系統行為,復雜系統的重要的大尺度行為并不是對小尺度行為的簡單平均。多尺度上的相關性使得人們不清楚小尺度的行為究竟是如何造成更大尺度的行為的。然而,即使是復雜的系統,大尺度行為的復雜度也大大低于小尺度行為的復雜度,大尺度行為往往不取決于系統的大部分細節(如圖9所示)。通常,了解復雜系統大尺度行為的關鍵是找到合適的數學(或概念性)描述,不是對于所有細節的簡單的平均,也不是對所有細節的全盤考慮[12]。
[12]譯者注:方福康教授在“神經系統復雜性研究中的幾個問題”一文中寫到,Prigogine學派的重要成員A.Babloyantz明確提出,在復雜的非線性多維系統中存在著一個少維子系統,在這個少維子系統中可以描述腦神經認知功能的基本規律。協同學創始人H. Haken教授曾指出,學習和模式識別過程是大腦不同狀態的躍遷,而這一過程可以利用少維的序參量來刻畫。T. Kohonen結合神經網絡與自組織理論,用映射的方法,將復雜、多維的大腦微觀構造約化為二維的平面結構,并構造出自組織特征映射模型(SOM),在一定程度上解釋了語言的特征及其障礙的產生機理。方福康教授認為這些理論工作的共同特點是,對復雜神經系統的認知活動進行某種抽象,將具有龐大維數的真實系統投影到少維空間,并在此基礎上進行可操作性的分析工作。這些研究在很多方面獲得了成功,表明了復雜系統概念和自組織理論是研究神經系統認知活動的很好的工具。
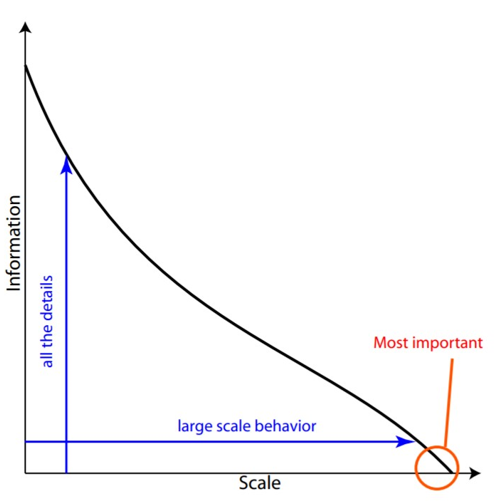
圖9. 一個復雜系統復雜度曲線示意圖。
在這,信息是復雜度的同義詞,因為復雜度就是在特定尺度上驅使系統行為必須的信息量。了解系統的所有細節(所有的微觀尺度的行為)是不可能也是不必要的。最重要的信息是大尺度行為所包含的。當然,對于平均場理論不適用的系統,弄清這些行為特征可能很困難。
第三部分、復雜系統與不確定性 (COMPLEX SYSTEMS AND UNCERTAINTY)
雖然前面的部分可以幫助我們了解系統的基本屬性和局限性,但我們對大多數復雜系統的理解不可避免地是不完善的。而且,無論有多周到的考慮方案,一個真正復雜的系統都會呈現出未提前納入考慮的要素。對于一個具有高復雜度的功能系統,任何一種改動,更可能帶來壞的影響而不是好的影響,例如改變計算機或者飛機中內的一條連線很可能讓系統不能工作。從這個角度來看,系統的高復雜度意味著可能只有一種配置是有效的,而其他配置方式都是無效的。如果缺乏完備的知識,如何確保我們設計或參與其中的系統能成功?雖然許多系統的成功基于正確決策的假設,但一些決策者容易犯錯誤(無論是由于腐敗,潛意識偏見還是人類思想的根本局限)的系統仍然表現良好。復雜系統的研究通過(隱式或顯式)將決策者本身視為系統的一部分并且具有有限的復雜性/決策能力,從而科學地處理這一問題。這樣一來,問題就成為:我們如何設計包含決策者而超出決策者本身復雜度的系統?
A. 進化過程(Evolutionary processes)
一個關鍵現象是,盡管不確定性(uncertainty)會使大多數系統變弱,但某些系統卻受益于不確定性和可變性(variability)。這些系統的共同特征是它們都體現出某種進化過程,即復制成功的變更(并進一步修改),而忽視或拋棄沒有成功的變更。經典的進化過程表現在生物學上:正是由于隨機突變導致的變異性,才最終使得具體人體這樣尺度和復雜度的機體逐步由單細胞生物體進化而來的。此外,人類自身也具有從隨機沖擊中受益的特點(前提是沖擊不會太強)。如:通過早期暴露于非致命性病原體,可提高免疫系統的性能;肌肉和骨骼會因為微挫或小的破損得以增強;我們通過接觸新信息和解決問題來學習;只要逆境不太嚴重,我們的心理就會因逆境而被鍛煉得更加強壯[13]。
[13]譯者注:最近發表的文章“The Eighty Five Percent Rule for Optimal Learning”,通過研究表明對于動物學習和人工神經網絡的學習在錯誤率為(error rate)達到15%左右時候最優,學習效率最高,暗示著這種可以帶來益處的不確定性和可變性具有一定的優化尺度(比率),太小則讓進化速度太慢,過大則缺乏足夠的穩定性,會讓系統失去前進的方向。
競爭性市場經濟提供了系統如何在不確定性條件下蓬勃發展的另一個例子。由于我們天生并不知道如何成功,必須同時創造和改進許多潛在的創新和業務,成功的創新和業務將擴大而不成功的創新和業務將被拋棄。這樣的過程將使成功的部分得到進一步改進。但是,如果沒有被有效監管的多尺度合作框架,經濟體系的大尺度部分可能會針對錯誤的目標進行優化,從而造成有害的社會均衡(harmful societal equilibria)。
同樣,大型組織的內部流程可以遵循這樣的演化模式,組織中的一小部分可能會失敗但整體會因此得到改善;而如果沒有這種靈活性(flexibility,),面對不斷變化的外部環境,整個組織可能會立即失敗。在某些情況下,整個組織的失敗為更有效的組織取代它提供了空間(假設經濟已充分分散且具有競爭力,因此所討論的組織不會有“太大而不能倒閉”的情況)。但是,政府的倒閉要盡量避免,因此,施政系統更應該本身具有一定的靈活性以從隨機性和不確定性中受益。不允許發生小的故障,就會終止進化過程并建立相互依存關系,長期來看會削弱系統的功能,最終導致系統風險(這或許違反大家的直覺,但確實如此)。
為了在不確定性中蓬勃發展并超越個體決策的復雜性,系統可以包含進化過程,即使它們最初非常有限,但它們會隨著時間的推移自然得到改善。一般來說,一個系統只能設計出復雜度更低的系統,但隨著時間推移,進化可以讓系統變得比其設計者變得更加復雜。要利用這個機制,需要做到如下兩點:
第一是允許系統中有足夠的變化,讓系統可以探索所有可能的空間。由于大量的變化意味著大的復雜度,而復雜度與尺度此消彼長,因此這種變化必須是在小尺度的空間和時間上發生。例如,對于一個施政系統,允許每個城市具有一定的獨立性,就可以讓它們同時并不斷地試行不同的方案。相反,如果讓國家的每個城市執行同樣的方案,結果就會差很多。
第二就是允許在系統的各個部分之間進行通信,以便在其他地方采用成功的選擇(例如,某個城市復制了其他城市的成功做法)。計劃總會有意想不到的后果;關鍵是要讓意想不到的后果對整個系統有利而不是有害。這需要經常放棄直接控制,以使復雜度可以隨時間自動增加。
B. 多尺度進化過程(Multi-scale evolutionary processes)
成功的進化過程通常不是只有無休止的競爭,而是包含著競爭和合作,這兩者均發生在多個尺度上。例如,細胞在多細胞生物內合作以更有效地與其他生物競爭,而生物會在物種內部和物種之間進行合作以更有效地與其他物種競爭。大尺度的競爭會自然地孕育小尺度的合作——為了使一個團隊有效地與另一個團隊競爭(在大尺度上競爭),必須在該團隊內部進行合作。合作也可以促進競爭——有時候,實現集團共同目標的最佳方法是鼓勵小集團之間的健康競爭。這些小集團又必須促進內部合作以有效地在子集團之間展開競爭,他們也可以通過在成員之間引入一些健康的競爭來提高內部合作的有效性。如果這些成員本身又是團體,則競爭引起合作再引起競爭的過程可以擴展到更小的尺度,具體過程如圖10所示。這個過程也可以反向進行:為了更有效地競爭,個人可以相互合作以形成團體,而團體又可以合作以形成更大的群體,依此類推。因此,各種規模(尺度)的團體之間合作與競爭的復雜網絡自然可以發展演變。
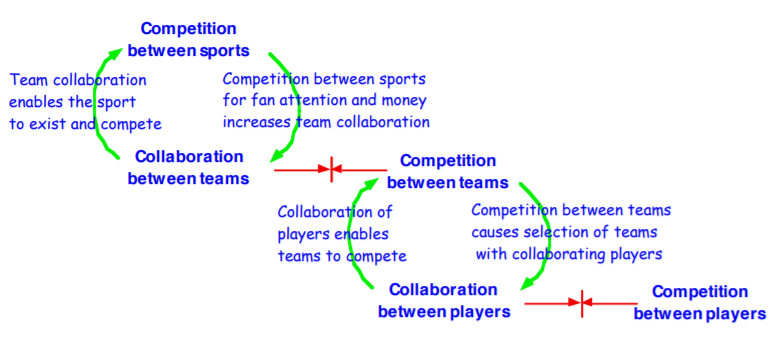
圖 10. 系統中的競爭與協作。集體中的競爭和協作的交替。
為了促進有效的團隊合作,競爭必須有合適的結構設計(properly structured)。一支足球隊的各個隊員以自己得分為目標,與團隊的其他成員競爭,這不會讓球隊取得更好的成績(有效),但讓隊員競爭“最佳球員”的頭銜可能會讓整個球隊更有競爭力。競爭必須設計得讓競爭者被激勵,讓他們做對集體更好的事情(可能有好有壞,但整體要好),否則會發生常見的悲劇。競爭可能會誤入歧途,這凸顯了要有多尺度結構的重要性(讓競爭在多個層次上發生),而不是讓系統中的每個人都與其他人競爭。市場經濟系統的成功不是因為自由市場產生最佳結果(現實世界中的市場通常會大大偏離自由市場模型的假設,并且具有很多外部性),而是讓內部盡其所能。適當監管的市場體系允許自然地發生多尺度的進化過程,使得創新和復雜性可以遠遠超出任何人的想象,更不用說設計者了。
總結
具有許多組元的系統通常表現出涌現行為,這是一種源自組元之間的關系而不是組元本身特征的行為。然而,統計物理學的早期見解是,盡管不可能描述數萬億個分子的細節,但通過分析這些分子狀態可能性的空間,而不是這些分子的運動等具體特征,就可以獲得對于宏觀性質的理解。盡管可以用分子的平均行為來描述許多宏觀特性,但是某些物理現象(例如相變)的宏觀特性不能通過對系統組元行為的平均來理解。因此,物理學家被迫開發新的多尺度研究方法。同樣,雖然標準的統計方法可以推斷出系統許多組成部分的平均屬性,甚至可以成功地對某些生物和社會系統進行建模,但這些方法對于其他系統更可能是失效的結果。
通過考慮可能的行為空間的系統視角,可能會對系統有更深入的洞察(insights),這是僅僅考慮特定問題或危機的大致因果關系所不能得到的。系統的復雜性,取決于系統潛在行為的數量(即可能性的空間),是把握大尺度特征的一個出發點,就像熵往往作為統計物理的出發點一樣。因為系統的不同行為的數量取決于細節的程度(如在較低分辨率下表現相同的行為,在較高分辨率下可能會不同),所以復雜度取決于尺度。組元之間的相互依賴會通過限制單個組元的自由度來減小系統在較小尺度上的復雜度。因此,對于由相同組元組成的系統,在小尺度和大尺度的行為數量之間存在根本的此消彼長(tradeoff)。這種尺度上和復雜度上的權衡關系到系統在適應性和效率之間的取舍抉擇,適應性取決于系統對小尺度擾動的響應多樣性,而效率則取決于系統可以運行的尺度(規模)。系統不存在必須具有某個復雜度的最優尺度,相反,最有效的系統需要在各個尺度上都與環境的復雜性相匹配。
在分析數據或創建組織結構時,傳統標準方法往往低估了組元相關的重要性以及由這些相互依賴性引起的復雜度,它們將不再適用。在某種程度上,可以通過將數據分析或組織結構與系統中的自然劃分進行匹配來緩解這些問題。由于復雜系統是行為發生在多個尺度上,因此對復雜系統成功的分析和組織本質上也必須是多尺度的。但是,即使配備了所有適當的信息和工具,人類對大多數復雜系統的理解也將不可避免地存在不足,系統具有不可預測性(with unpredictability being the best prediction)。為了面對這個現實,我們必須設計系統具有這樣的能力,它能像進化過程一樣被不可預測性增強而不是削弱。這樣的系統是靈活的,可以同時執行多個過程,并讓這些過程在多尺度合作框架內相互競爭,讓有效的行為在系統中得到復制傳遞。只有這種隨著時間的流逝通過不斷嘗試和試錯而變得越來越復雜的系統,才能達到可以解決超出人類理解能力極限的復雜問題的復雜度。